Конспект УЗ
МАТЕМАТИКА И ОБОРОНА СТРАНЫ Цели: воспитание у учащихся патриотизма, необходимости глубоких знаний математики в военном деле, знакомство с вкладом математиков в усиление оборонной мощи нашей страны.
На внеклассном мероприятии присутствуют учащиеся 5-8 классов, классы малочисленные, но в каждом классе есть сильные и любознательные ученики.
Данное УЗ проводится как внеклассное мероприятие, где встречается математический материал, охватывающий знания всей группы классов (5-8 кл).
Оборудование компьютер, мультимедийная установка.
Необходимые навыки владения ИКТ поиск информации в сети Интернет подбор картинок к тексту, создание и оформление слайдов с текстом и картинками.
I. Вступление.
В этом году 9 мая наша страна будет отмечать 65-ю годовщину Победы в Великой Отечественной войне с фашизмом.
65 лет прошло с того дня, когда в каждый наш дом, в каждую семью пришло выстраданное в жесточайших боях с фашизмом счастье Победы, счастье мира. Но сколько бы лет ни было позади, в памяти десятков народов Европы навсегда останется беспримерный подвиг советского солдата, спасший мир от «коричневой чумы» фашизма.
Готовясь отметить 65-ю годовщину Победы, мы снова и снова вспоминаем, какие суровые испытания выпали на долю нашей страны с той минуты, когда фашистские полчища вероломно, без объявления войны хлынули через наши границы. Сто девяносто дивизий, тысячи самолётов, танков и орудий были брошены на нашу землю с одной изуверской целью - давить, сжигать, беспощадно уничтожать всё, что встретится на пути.
«Всё для фронта, всё для победы!»- было призывом для каждого жителя нашей страны, которые стремились помочь Родине в борьбе с врагом. С этим призывом на фронт уходили тысячи добровольцев, формировались дивизии народного ополчения, партизанские отряды. Женщины, старики, подростки заменяли уходящих на заводах и колхозных полях, на строительстве оборонительных сооружений.
О железную стойкость советских людей, воинов Вооружённых Сил разбивались бронированные полчища гитлеровцев, а в битве под Москвой осенью 1941 года гитлеровцы потерпели первое во второй мировой войне крупное поражение, развеяв легенду о «непобедимости» фашистской армии.
1418 долгих дней и ночей длилась эта страшная война. Приблизить час Победы стремились все люди нашей страны. И вот сегодня мы расскажем вам о том, как учёные математики приблизили час Победы, сохранив жизни советским воинам и технику.
II. Основная часть.
23 июня 1941 года состоялось расширенное заседание Президиума Академии наук СССР. Советские учёные заявили, что отдадут «все свои знания, все свои силы, энергию и свою жизнь за дело нашего великого народа, за победу над врагом и полный разгром фашистских бандитов, осмелившихся нарушить священную границу нашей Родины».
Математический институт Академии наук СССР разрабатывает штурманские таблицы. Уже в 1943 году они находят широкое применение в боевой практике авиации дальнего действия. Какая ценность? Расчёты всех дальних полётов, выполняемые по этим таблицам, значительно повысили точность вождения самолётов.
1. Идёт ожесточённая война. Фронт требует увеличения эффективности огня артиллерии, повышения меткости стрельбы. Важная проблема. Её успешно решает академик А.Н.Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наиболее выгодного рассеяния артиллерийских снарядов. Это ещё не всё. Математическая теория вероятностей использовалась во время Великой Отечественной войны и для определения наилучших методов нахождения самолётов, подводных лодок противника, и для указания путей, позволяющих избежать встречи с подводными лодками врага.
Возьмём задачу «Как лучше провести караван торговых судов по океану, в котором действуют вражеские подводные лодки?» Задача не из лёгких! Если составить караван из большого числа судов, то вероятность встречи с подводными лодками противника будет меньшей. Это одно, но нельзя забывать другого: увеличатся потери, если встреча большого каравана судов осуществится с подводными лодками противника. Тут математика пришла на помощь. Её методами были определены размеры каравана судов и частота их отправления, при которых потери были бы наименьшими. Учёные-математики помогли рассчитать, сколько нужно сделать одновременно выстрелов по самолётам противника для того, чтобы иметь наибольшую вероятность попадания.
Во всём этом большая заслуга математической школы академика А.Н.Колмогорова.
Во время Великой Отечественной войны появилась и такая важная проблема, как обеспечение кучности стрельбы и устойчивости снарядов при полёте. Эту сложную математическую задачу решил член-корреспондент АН СССР Н.Г.Четаев. Он рассчитал наивыгоднейшую крутизну нарезки стволов орудий, что позволило обеспечить кучность и устойчивость снарядов пи полёте.
2. Война требовала от авиации больших скоростей самолётов, но увы! При освоении больших скоростей авиация столкнулась с внезапным разрушением самолётов от вибрации особого рода – флаттера. Опять новая проблема, которую немедленно надо решать. И тут на помощь приходят математики. За решение данной задачи берётся группа учёных во главе с М.В.Келдышем, она разработала сложную математическую теорию флаттера. Сделано большое дело: самолёты обеспечены защитой от появления вибраций.
3. Видная роль в обороне нашей Родины принадлежит выдающемуся академику математику А.Н.Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими славными Военно-Морскими Силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или других отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
В годы Великой Отечественной войны подготовка боевых операций, а их было много, была сопряжена с огромным количеством расчётов, которые требовали хороших знаний по математике.
4. На современном этапе развития в условиях возможной войны объём вычислительных работ становится неизмеримо больше. Теперь на вооружении Военно-Воздушных Сил находится множество ракет различного назначения. В составе Военно-Морского Флота входят новые атомные подводные лодки-ракетоносцы, оснащённые баллистическими ракетами с подводным стартом.
Как видно, оружие стало очень сложным, мощным и результативным, поэтому неизмеримо возросла мера ответственности за его применение. Точность попадания ракеты в цель во многом зависит от качества выполнения необходимых математических расчётов. Это усложнило деятельность каждого командира и, в конечном счёте, всю задачу управления войсками. Отсюда, чтобы умело руководить войсками, командные кадры должны иметь знания по математике, уметь широко использовать вычислительные средства.
Теперь многие вопросы управления войсками, ракетным оружием решаются в исключительно сжатые сроки. В этом деле очень много помогают математические машины.
III. Викторина.
Попытаемся и мы в сегодняшней викторине проявить смекалку, находчивость, умение хорошо производить расчёт.
См.на слайдах 8-13.
IV. Занимательные задачи.
1. Задача о партизанах.
Группу партизан в 68 человек во главе 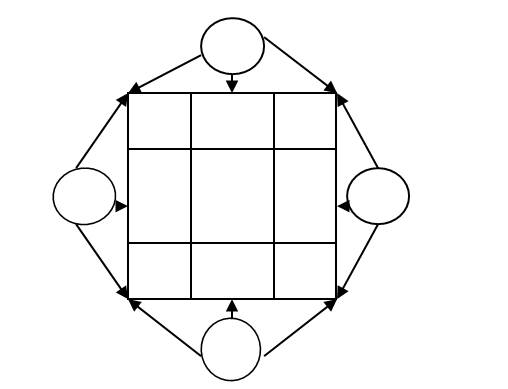
с учителем математики Сидоренко
внезапно окружил противник.
Их привезли в родное село и закрыли
в здании клуба, назначив на следующий
день суд. В центре клуба был зрительный
зал, а вокруг него 8 смежных между
собой комнат с окнами на улицу.
Командир противника поставил
у четырёх сторон здания часовых,
а пленных партизан разместил в
комнатах так, чтобы каждый часовой
видел из окна 21 партизана одновременно.
Приказав каждому часовому следить за тем, чтобы это число охраняемых им партизан не уменьшилось, командир назначил смену караула через 3 часа и ушёл в штаб. Перед Сидоренко встали вопросы: что делать, как предупредить партизанский отряд, что село занято противником, как спасти свою группу от плена? Он знал, что под сценой зрительного зла есть подвал с выходом в сарай, где хранились декорации. Через этот ход можно было выйти из клуба. Однако, взяв из охраняемых комнат хотя бы одного человека, он мог бы вызвать тревогу, т.к. часовые непрерывно смотрели в окна и пересчитывали своих пленных. Сидоренко сообразил, что если в момент смены караула сделать перестановку пленников в комнатах, то незаметно для часовых он сможет каждый раз освобождать нескольких человек, которые пройдут под сценой в сарай, а затем в отряд. Так было и сделано.
Во время смены караула Сидоренко перегруппировал партизан и освободил 8 человек, а затем 3 раза ещё по 4 человека. Он подготовил и ещё пятую группу из 4 человек, но в это время в село вошёл предупреждённый партизанский отряд, который уничтожил противника и освободил всех остальных партизан.
Как Сидоренко размещал своих друзей по комнатам, чтобы освободить в 5 приёмов24 человека, в то время как на глазах у каждого вновь заступившего часового на каждой стороне здания всегда было по 21 партизану?
2. Задача о переправе.
Небольшая группа солдат подошла к реке, на берегу которой была маленькая лодка и 2 мальчика. Как с помощью мальчиков и лодки отряд переправился на другой берег, если в лодку может сесть один солдат или два мальчика?
3. Математический фокус.
Ученик говорит: «Пусть любой желающий напишет на бумажке любое трёхзначное число, которое я угадаю после того, как вы выполните следующие действия:
1) припишите к нему это же число ещё раз, получится, конечно, шестизначное число:
2) передайте бумажку соседу, что сидит подальше от меня, а он пусть разделит это шестизначное число на семь;
3) результат вручите своему соседу, не сообщая мне, пусть он разделит этот результат на 11;
4) передайте результат дальше. Разделим его… ну, скажем, на 13;
5) дайте мне бумажку с результатом, только сложите её так, чтобы я не видел числа».
Не развёртывая листа бумаги, «фокусник» вручает его тому, кто задумал число, со словами: «Извольте получить задуманное число».
«Фокусник» даёт разгадку. Ведущий закрывает встречу.
Литература
1. Газета «Математика», №7, 1998г., Приложение к газете «Первое сентября».
2. Журнал «Математика в школе», №3, 1972г.
3. Е.Г.Козлова «Сказки и подсказки».
4. Е.И.Игнатьев «В царстве смекалки».
5. Н.К.Смышляев «О математике и математиках».
6. А.Г.Конфорович. Советские математики в годы Великой Отечественной войны. (Математика в школе. – 1975.-№2)
7. Б.В.Гнеденко. «Математика и оборона страны». (Математика в школе.-1978.-№2).
8. М.А.Андреева. Урок, посвящённый дню Победы. (Математика в школе.-2003.- №4).
Источник: http://www.scribd.com/full/27171656?access_key=key-1xo19vrxf5oe9qsgwqeb |

